
Framewise from left to right: 1 2 3 4 5 6
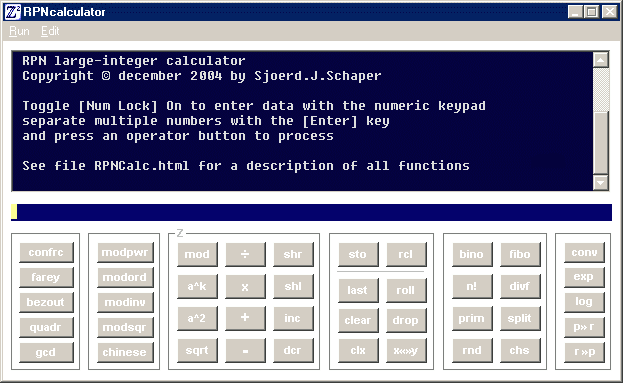
{confrc}
Continued fraction representation of rational a ⁄ b,
truncated at the last convergent p ⁄ q with q ≤ n.
In: Z(a), Y(b), X(n); out: Y(p), X(q), Textbox(partial quotients).
{farey}
Find the successor of rational a ⁄ b in the Farey series of order n:
the ascending series of irreducible fractions with denominators ≤ n.
In: Z(a), Y(b), X(n); out: Y(p), X(q).
{bezout}
Find the smallest solution of indeterminate equation a · x + b · y = c
(aka. Bézout's identity), equivalent to the congruence b · y ≡ c (mod a).
The gcd(a, b) must divide c. Input c = 0 to compute a · x + b · y = gcd(a, b).
In: Z(a), Y(b), X(c); out: Y(x), X(y).
{quadr}
The smallest real solution of quadratic equation a · x² + b · x = c
in rational approximation p ⁄ q.
In: Z(a), Y(b), X(c); out: Y(p), X(q), Textbox(decimal expansion).
{gcd}
Greatest common divisor of integers a and b: the largest positive integer
which divides both a and b. Press {÷} {×} to obtain the least common multiple.
In: Y(a), X(b); out: Z(a), Y(b), X(gcd).
To retain the modulus in the next five functions, it must be input as first argument.
{modpwr}
Modular exponentiation: raise base a to the k-th power and reduce modulo m.
In: Z(m), Y(a), X(k); out: Y(m), X(power).
{modord}
Calculate the Euler totient function φ(m) and the order of a modulo m:
the smallest positive value of x for which a^x ≡ 1 (mod m).
This fails if a and m are not coprime or if the calculator cannot factorize m.
Press F1 to break off, repeat if necessary.
If base a = 1, then the order is set to φ(m).
If φ(m) is equal to the Carmichael λ-function for m,
then the least positive primitive root of m is also given.
In: Y(m), X(a);
out: Z(m), Y(a), X(x), Textbox(φ(m) and either λ(m) or the root).
{modinv}
Multiplicative inverse or associate of a to modulus m: x such that a · x ≡ 1 (mod m).
This fails if a and m are not coprime.
In: Y(m), X(a); out: Y(m), X(x).
{modsqr}
Calculate Kronecker's symbol for a and m, and solve quadratic congruence x² ≡ a (mod m).
This fails if a is a quadratic nonresidue modulo m
or if m is composite and cannot be factorized by the calculator.
In: Y(m), X(a); out: Y(m), X(x), Textbox((a ⁄ m)).
{chinese}
Find the solution of simultaneous congruences x ≡ a (mod m) and x ≡ b (mod n)
with the Chinese remainder theorem. This fails if gcd(m, n) does not divide b − a.
In: R(m), Z(a), Y(n), X(b); out: Y(modulus), X(x).
This frame may be switched into different calculation modes by clicking it.
{mod}
Residue of a to modulus m: positive solution of x ≡ a (mod m).
In: Y(a), X(m); out: X(x).
In: R(a), Z(b), Y(p), X(q);
out: Y(aq mod bp), X(bq).
In: R(a), Z(b), Y(u), X(v);
out: Y(x), X(y),
with x + yi = w − round(w ⁄ z) × z, w = a + bi, z = u + vi.
{a^k}
Exponentiation: raise base a to the k-th power.
In: Y(a), X(k); out: X(power).
In: Z(a), Y(b), X(k);
out: Y(a^k), X(b^k), k ∈ ℕ.
In: Z(a), Y(b), X(k);
out: Y(x), X(y),
with x + yi = (a + bi)^k, k ∈ ℕ.
{a^2}
The square of a.
In: X(a); out: X(square).
In: Y(a), X(b);
out: Y(a^2), X(b^2).
In: Y(a), X(b);
out: Y(x), X(y),
with x + yi = (a^2 + b^2) + 2abi.
{sqrt}
Integer square root of a ≥ 0.
In: X(a); out: X(root).
In: Y(a), X(b);
out: Y(√a), X(√b).
In: Y(a), X(b);
out: Y(x), X(y),
with x + yi = (a + bi)^½.
{÷}
Integer division.
In: Y(a), X(b); out: X(a ⁄ b).
In: R(a), Z(b), Y(p), X(q);
out: Y(aq), X(bp).
In: R(a), Z(b), Y(u), X(v);
out: Y(x), X(y),
with x + yi = (au + bv) ⁄ t + i(bu − av) ⁄ t, t = u^2 + v^2.
{×}
Multiplication.
In: Y(a), X(b); out: X(a × b).
In: R(a), Z(b), Y(p), X(q);
out: Y(ap), X(bq).
In: R(a), Z(b), Y(u), X(v);
out: Y(x), X(y),
with x + yi = (au - bv) + i(bu + av).
{+}
Addition.
In: Y(a), X(b); out: X(a + b).
In: R(a), Z(b), Y(p), X(q);
out: Y(aq + bp), X(bq).
In: R(a), Z(b), Y(u), X(v);
out: Y(a + u), X(b + v).
{−}
Subtraction.
In: Y(a), X(b); out: X(a − b).
In: R(a), Z(b), Y(p), X(q);
out: Y(aq − bp), X(bq).
In: R(a), Z(b), Y(u), X(v);
out: Y(a − u), X(b − v).
{shr}
Shift a one bit to the right.
In: X(a); out: X(a ⁄ 2).
In: Y(a), X(b);
out: Y(a), X(b × 2).
In: Y(a), X(b);
out: Y(a ⁄ 2), X(b ⁄ 2).
{shl}
Shift a one bit to the left.
In: X(a); out: X(a × 2).
In: Y(a), X(b);
out: Y(a × 2), X(b).
In: Y(a), X(b);
out: Y(a × 2), X(b × 2).
{inc}
Increment a by one.
In: X(a); out: X(a + 1).
In: Y(a), X(b);
out: Y(a + 1), X(b).
In: Y(a), X(b);
out: Y(a + 1), X(b).
{dcr}
Decrement a by one.
In: X(a); out: X(a − 1).
In: Y(a), X(b);
out: Y(a − 1), X(b).
In: Y(a), X(b);
out: Y(a − 1), X(b).
{sto}
Store the contents of registers X (display) and Y (stack bottom) into memory.
{rcl}
Recall the memory contents and put them into registers X and Y.
[Enter] (has no button equivalent)
Save the value in the display (copy register X to Y and lift the stack).
{last} or [Up Arrow]
Exchange the current stack with the stack before the last operation.
{clear} or [Insert]
Clear the current stack.
{clx} or [Delete]
Cancel entry (clear the display).
{roll} or [Page Up]
Roll the stack one level up.
{drop} or [Page Down]
Drop the stack one level down.
{x«»y} or [Down Arrow]
Swap the X (display) and Y (stack bottom) registers.
{bino}
Binomial coefficient or combination n choose k: the coefficient of x^k
in (1 + x)^n, also the number of k-subsets possible out of a set of n
distinct items. Positive k ≤ abs(n) < 10^9.
In: Y(n), X(k); out: X(binomial coefficient).
{n!}
Factorial of integer abs(n): the number of ways in which n objects
can be permuted, defined as n · (n − 1) · · · 2 · 1.
In: X(n); out: X(factorial).
{prim}
Find the next probable prime ≥ abs(a) with the 1980 Miller-Rabin
strong pseudoprime test. Press F1 to break off.
In: X(a); out: X(next prime).
{rnd}
Random positive integer a with length abs(l).
In: X(l); out: X(random a).
{fibo}
Fibonacci number Fn, defined by the recurrence relation Fn+1 = Fn + Fn-1,
with F1 = F2 = 1 and index abs(n).
In: X(n); out: X(Fn).
{divf}
Divisor functions μ(a), ω(a), Ω(a), δ(a) and σ(a) of nonzero integer abs(a).
This fails if the calculator cannot factorize a. Press F1 to break off.
In: X(a); out: Y(σ(a)), Textbox(prime factors and function values).
{split}
Attempt to split abs(a) in two (composite) factors. Press F1 to break off.
If a is prime and a ≡ 1 (mod 4) then abs(a) is factored into
conjugate Gaussian primes x ± yi in the quadratic ring K = ℤ[i].
The continued fraction expansion of a ⁄ r, with r² ≡ −1 (mod a) is also given.
In: X(a); out: Y(f or x), X(a ⁄ f or y), Textbox(partial quotients).
{chs} or left [-]
Change the sign of integer a.
In: X(a); out: X(-a).
{conv}
Convert rational number a ⁄ b to base n.
In: if 2 ≤ register X ≤ 17: Z(a), Y(b), X(n)
otherwise Y(a), X(b), n = 10; out: Textbox(expansion in base n).
{exp}
Rational approximation p ⁄ q of exponential function(a ⁄ b).
In: Y(a), X(b); out: Y(p), X(q), Textbox(decimal expansion).
{log}
Rational approximation p ⁄ q of natural logarithm(a ⁄ b).
In: Y(a), X(b); out: Y(p), X(q), Textbox(decimal expansion).
{p» r}
Rational polar to rectangular coordinates or
absolute value r ⁄ s and argument a ⁄ b to vector (x, y) and denominator (d, 0).
In: R(r), Z(s), Y(a), X(b); out: R(x), Z(y), Y(d), X(0), Textbox(decimal expansion).
{r »p}
Rectangular to rational polar coordinates or
vector (x, y) to absolute value r ⁄ s and argument a ⁄ b.
In: Y(x), X(y); out: R(r), Z(s), Y(a), X(b), Textbox(decimal expansions).
To change the decimal precision for the above 5 functions and {quadr},
input 10 ≤ size ≤ 1000 in register X and press [Ctrl]+E.
The included bignumVB.dll is compiled with a 64K-word number array,
good for max. 16K-digit largeints: big enough for most purposes,
while even larger numbers would make a rather unwieldy stack.
If this is too restrictive, then recompile largeint.bas with Asize increased.
A number is first divided by all primes < 2^17, then the Pollard-Brent
Monte Carlo rho-algorithm is applied to the residue. Successive random
mappings are continued for 2^16 iterations each, until a factor is found.
The splitting process is then repeated recursively. Most numbers with
up to 25 figures will be fully factorized, bigger ones only if they're smooth.